Soalan 20 (4 markah):
Jadual 1 menunjukkan taburan markah bagi 40 orang murid dalam ujian Matematik Tambahan. Bilangan murid bagi selang kelas 40 – 59 tidak dinyatakan.
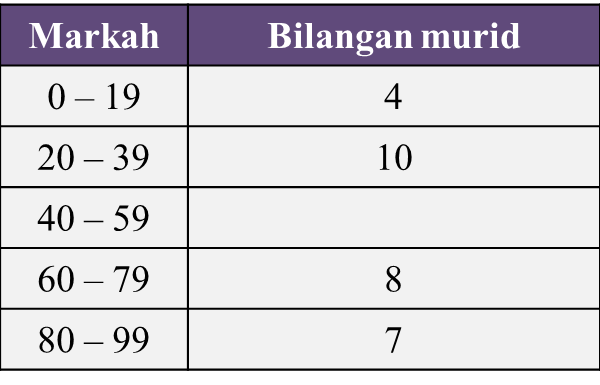 Jadual 1
Jadual 1
(a) Nyatakan kelas mod.
(b) Puan Zainon, guru mata pelajaran, berhasrat untuk memberi ganjaran kepada sepuluh murid terbaik. Murid-murid yang mencapai markah minimum dalam kedudukan sepuluh terbaik akan dipertimbangkan untuk menerima ganjaran tersebut. Elina memperoleh 74 markah.
Adakah Elina layak dipertimbangkan untuk menerima ganjaran itu? Beri sebab anda.
Solution:
(a)
4 + 10 + x + 8 + 7 = 40
x + 29 = 40
x = 11
Kelas mod = 40 – 59
(b)
Jadual 1 menunjukkan taburan markah bagi 40 orang murid dalam ujian Matematik Tambahan. Bilangan murid bagi selang kelas 40 – 59 tidak dinyatakan.
 Jadual 1
Jadual 1(a) Nyatakan kelas mod.
(b) Puan Zainon, guru mata pelajaran, berhasrat untuk memberi ganjaran kepada sepuluh murid terbaik. Murid-murid yang mencapai markah minimum dalam kedudukan sepuluh terbaik akan dipertimbangkan untuk menerima ganjaran tersebut. Elina memperoleh 74 markah.
Adakah Elina layak dipertimbangkan untuk menerima ganjaran itu? Beri sebab anda.
Solution:
(a)
4 + 10 + x + 8 + 7 = 40
x + 29 = 40
x = 11
Kelas mod = 40 – 59
(b)
Soalan 21 (3 markah):
sebiji dadu berbentuk kubus yang tidak adil dilambung. Kebarangkalian mendapat angka ‘4’ ialah dan kebarangkalian mendapat selain daripada nombor ‘4’ adalah sama antara satu sama lain.
Jika dadu itu dilambung dua kali, cari kebarangkalian mendapat dua nombor yang berlainan.
Beri jawapan anda dalam bentuk pecahan termudah.
Penyelesaian:
sebiji dadu berbentuk kubus yang tidak adil dilambung. Kebarangkalian mendapat angka ‘4’ ialah dan kebarangkalian mendapat selain daripada nombor ‘4’ adalah sama antara satu sama lain.
Jika dadu itu dilambung dua kali, cari kebarangkalian mendapat dua nombor yang berlainan.
Beri jawapan anda dalam bentuk pecahan termudah.
Penyelesaian:
Soalan 22 (4 markah):
Danya mempunyai sebuah kedai barangan perhiasan rumah. Pada suatu hari, Danya menerima 14 set cawan daripada seorang pembekal. Setiap set mengandungi 6 biji cawan yang berlainan warna.
(a) Danya memilih 3 set cawan secara rawak untuk diperiksa.
Cari bilangan cara yang berlainan yang digunakan oleh Danya untuk memilih set-set cawan itu.
(b) Danya mengambil satu set cawan untuk dipamerkan dengan menyusunnya secara sebaris.
Cari bilangan cara yang berlainan cawan-cawan itu boleh disusun dengan keadaan cawan berwarna biru tidak diletak bersebelahan cawan berwarna merah.
Penyelesaian:
(a)
Bilangan cara yang berlainan yang digunakan oleh Danya untuk memilih 3 set cawan secara rawak untuk diperiksa
= 14C3
=364
(b)

Bilangan cara (Cawan berwarna biru diletak bersebelahan cawan berwarna merah)
= 5! × 2!
= 240
Bilangan cara yang berlainan cawan berwarna biru tidak diletak bersebelahan cawan berwarna merah
= 6! – 240
= 720 – 240
= 480
Danya mempunyai sebuah kedai barangan perhiasan rumah. Pada suatu hari, Danya menerima 14 set cawan daripada seorang pembekal. Setiap set mengandungi 6 biji cawan yang berlainan warna.
(a) Danya memilih 3 set cawan secara rawak untuk diperiksa.
Cari bilangan cara yang berlainan yang digunakan oleh Danya untuk memilih set-set cawan itu.
(b) Danya mengambil satu set cawan untuk dipamerkan dengan menyusunnya secara sebaris.
Cari bilangan cara yang berlainan cawan-cawan itu boleh disusun dengan keadaan cawan berwarna biru tidak diletak bersebelahan cawan berwarna merah.
Penyelesaian:
(a)
Bilangan cara yang berlainan yang digunakan oleh Danya untuk memilih 3 set cawan secara rawak untuk diperiksa
= 14C3
=364
(b)

Bilangan cara (Cawan berwarna biru diletak bersebelahan cawan berwarna merah)
= 5! × 2!
= 240
Bilangan cara yang berlainan cawan berwarna biru tidak diletak bersebelahan cawan berwarna merah
= 6! – 240
= 720 – 240
= 480