Soalan 7:
Penyelesaian secara lukisan berskala tidak diterima.
Rajah di bawah menunjukkan segi tiga PRS. Sisi PR bersilang dengan paksi-y pada titik Q.
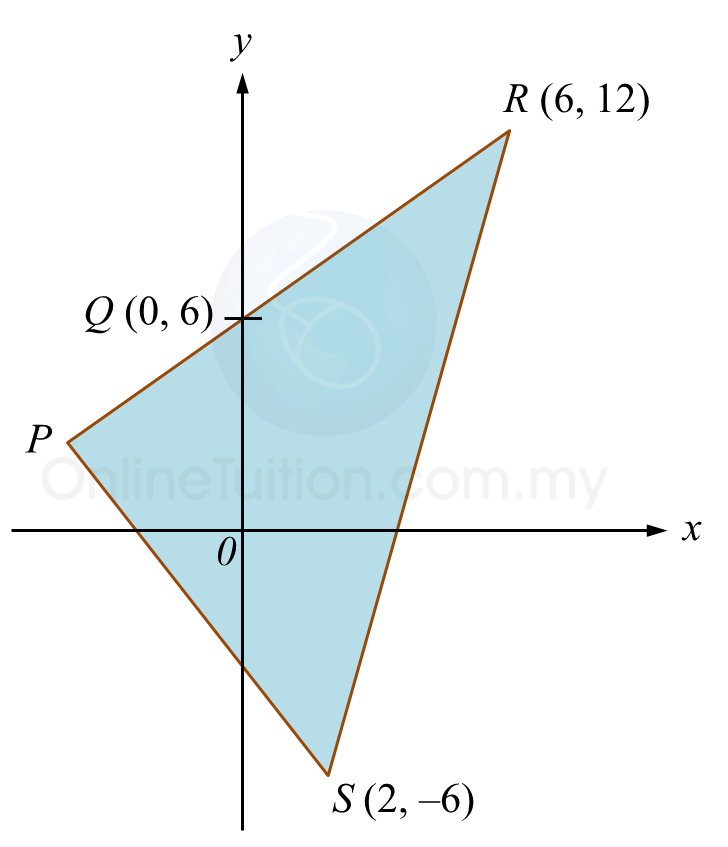
(a) Diberi PQ : QR = 2 : 3, cari
(i) koordinat P,
(ii) persamaan garis lurus PS,
(iii) luas, dalam unit2, segi tiga PRS.
(b) Titik M bergerak dengan keadaan jaraknya dari titik R adalah sentiasa dua kali jaraknya dari titik S.
Cari persamaan lokus M.
Penyelesaian:
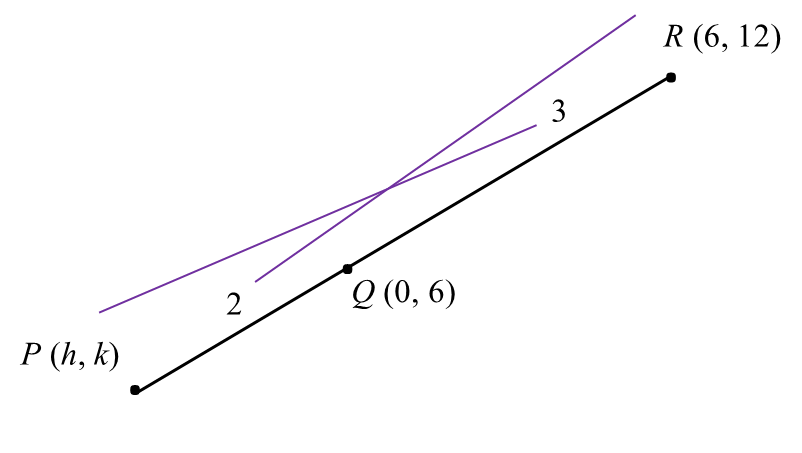
(a)(ii)
(a)(iii)
(b)
Penyelesaian secara lukisan berskala tidak diterima.
Rajah di bawah menunjukkan segi tiga PRS. Sisi PR bersilang dengan paksi-y pada titik Q.

(a) Diberi PQ : QR = 2 : 3, cari
(i) koordinat P,
(ii) persamaan garis lurus PS,
(iii) luas, dalam unit2, segi tiga PRS.
(b) Titik M bergerak dengan keadaan jaraknya dari titik R adalah sentiasa dua kali jaraknya dari titik S.
Cari persamaan lokus M.
Penyelesaian:
(a)(i)

(a)(ii)
(a)(iii)
(b)
Soalan 8:
Rajah di bawah menunjukkan sisi empat ABCD. Titik C terletak pada paksi-y.
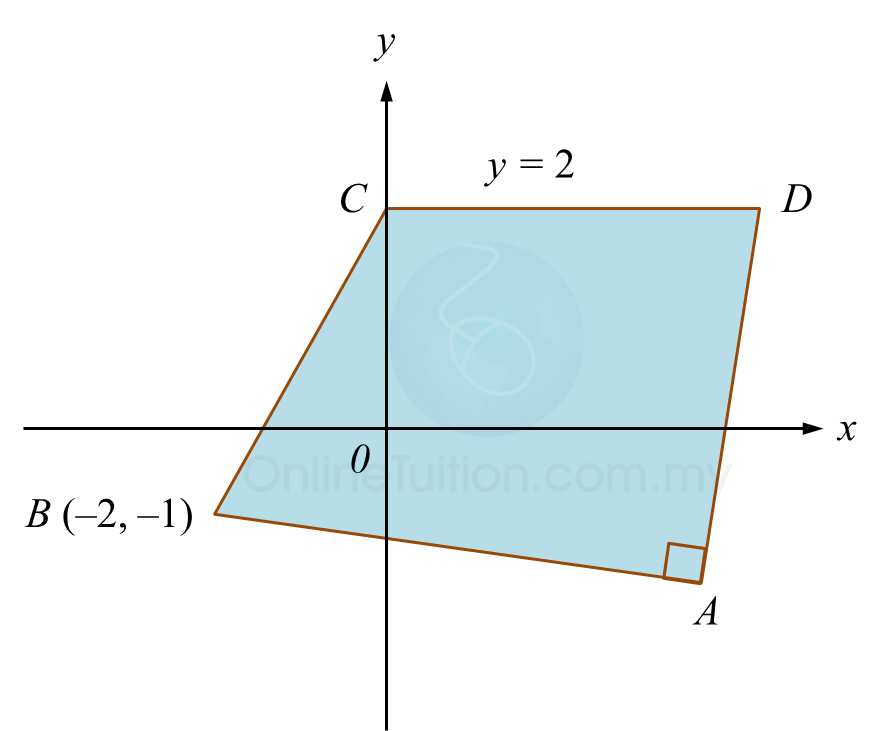
Persamaan garis lurus AD ialah 2y = 5x – 21.
(a) Cari
(i) persamaan garis lurus AB,
(ii) koordinat A,
(b) Titik P bergerak dengan keadaan jaraknya dari titik D sentiasa 5 unit.
Cari persamaan lokus P.
Penyelesaian:
(a)(ii)
(b)
Rajah di bawah menunjukkan sisi empat ABCD. Titik C terletak pada paksi-y.

Persamaan garis lurus AD ialah 2y = 5x – 21.
(a) Cari
(i) persamaan garis lurus AB,
(ii) koordinat A,
(b) Titik P bergerak dengan keadaan jaraknya dari titik D sentiasa 5 unit.
Cari persamaan lokus P.
Penyelesaian:
(a)(i)
(a)(ii)
(b)