7.8.3 Geometri Koordinat, SPM Praktis (Kertas 2)

Soalan 5:

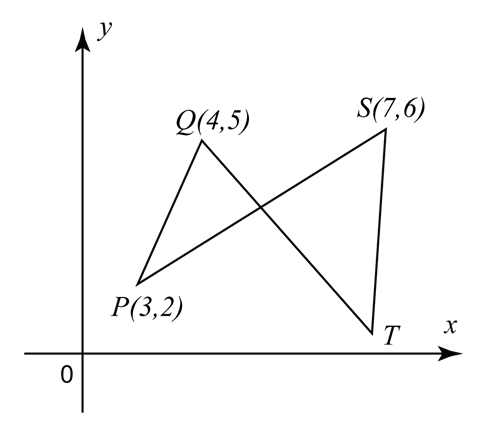
Dalam rajah di atas, PRS dan QRT ialah garis lurus. Diberi R adalah titik tengah bagi PS dan
QR : RT = 1 : 3, Cari

(a) koordinat titik R,

(b) koordinat titik T,

(c) koordinat bagi titik persilangan antara garis PQ dan garis ST.

Penyelesaian:

(a)

Diberi R ialah titik tengah bagi PS.

\begin{array}{l} R = (\frac{3 + 7}{2}, \frac{2 + 6}{2}) \\ R = (5, 4) \end{array}

(b)

QR : RT = 1 : 3

Katakan koordinat titik T = (x, y)

\begin{array}{l} (\frac{(1) (x) + (3) (4)}{1 + 3}, \frac{(1) (y) + (3) (5)}{1 + 3}) = (5, 4) \\ \frac{x + 12}{4} = 5 \\ x + 12 = 20 \\ x = 8 \\ \frac{y + 15}{4} = 4 \end{array}

y + 15 = 16

y = 1

T = (8, 1)

(c)

Kecerunan P Q = \frac{5 - 2}{4 - 3} = 3

Persamaan PQ,

y – 2 = 3 (x – 3)

y – 2 = 3x – 9

y = 3x – 7 ---- (1)

Kecerunan S T = \frac{6 - 1}{7 - 8} = - 5

Persamaan ST,

y – 1 = –5 (x – 8)

y – 1 = –5x + 40

y = –5x + 41 ---- (2)

Gantikan (1) ke dalam (2),

3x – 7 = –5x + 41

8x = 48

x = 6

Dari (1),

y = 3(6) – 7 = 11

Koordinat bagi titik persilangan antara garis PQ dan garis ST = (6, 11).

Soalan 6:

Penyelesaian secara lukisan berskala tidak akan diterima.

Rajah di bawah menunjukkan sebuah segi tiga OPQ. Titik S terletak pada garis PQ.

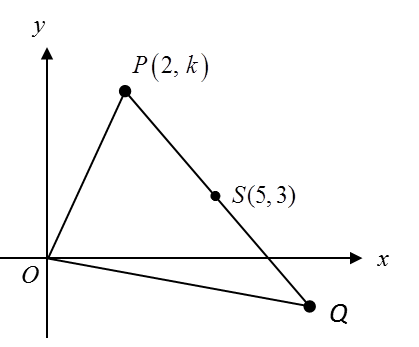
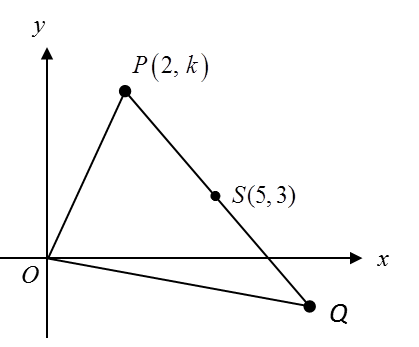
(a) Suatu titik Y bergerak dengan keadaan jaraknya dari titik S adalah sentiasa 5 uint. Cari persamaan lokus Y.
(b) Diberi bahawa titik P dan titik Q terletak pada lokus Y.

Hitung
(i) nilai k,
(ii) koordinat Q.

(c) Seterusnya, cari luas, dalam uint², bagi segi tiga OPQ.

Penyelesaian:

(a)

Katakan koordinat titik Y ialah (x, y), dan YS = 5 unit

\sqrt{{(x - 5)}^{2} + {(y - 3)}^{2}} = 5

x² – 10x + 25 + y² – 6y + 9 = 25

x² + y² – 10x – 6y + 9 = 0

(b)(i)

Diberi titik P (2,k) terletak pada lokus Y

(2)² + (k)²– 10 (2) – 6 (k) + 9 = 0

4 + k² – 20 – 6k + 9 = 0

k² – 6k – 7 = 0

(k – 7) (k + 1) = 0

k = 7 atau k = –1

Berdasarkan rajah, k = 7

(b)(ii)

Diberi P dan Q terletak pada lokus Y, S ialah titik tengah PQ. P = (2, 7), S = (5, 3)

Katakan koordinat Q = (x, y),

\begin{array}{l} (\frac{2 + x}{2}, \frac{7 + y}{2}) = (5, 3) \\ \frac{2 + x}{2} = 5 dan \frac{7 + y}{2} = 3 \end{array}

2 + x = 10 dan 7 + y= 6

x = 8 dan y = –1

Koordinat Q = (8, –1).

(c)

Luas ∆ OPQ

\begin{array}{l} = \frac{1}{2} | \begin{array}{l} 0 8    2 \\ 0 - 17 \end{array} \begin{array}{l} 0 \\ 0 \end{array} | \\ = \frac{1}{2} | 0 + (8) (7) + 0 - 0 - (- 1) (2) - 0 | \\ = \frac{1}{2} | 58 | \\ = 29 {unit}^{2} \end{array}

Leave a Comment Cancel reply