3.8.2 Pengamiran, SPM Praktis (Kertas 2)

Soalan 3:

Fungsi kecerunan suatu lengkung melalui titik P(2, -14) ialah 6x² – 12x.

Cari

(a) persamaan lengkung itu,

(b) koordinat titik-titik pusingan lengkung itu, dan tentukan sama ada setiap titik pusingan itu adalah maksimum atau minimum.

Penyelesaian:

(a)

Fungsi kecerunan suatu lengkung, dy/dx = 6x² – 12x

persamaan lengkung,

\begin{array}{l} y = \int (6 x^{2} - 12 x) d x \\ y = \frac{6 x^{3}}{3} - \frac{12 x^{2}}{2} + c \end{array}

y = 2x³ – 6x² + c

–14 = 2(2)³ – 6(2)² + c, di titik P (2, –14)

–14 = –8 + c

c = –6

y = 2x³ – 6x² – 6

(b)

dy/dx = 6x² – 12x

Di titik pusingan, dy/dx = 0

6x² – 12x = 0

6(x – 2) = 0

x = 0, x = 2

x = 0, y = 2(0)³ – 6(0)² – 6 = –6

x = 2, y = 2(2)³ – 6(2)² – 6 = –14

\begin{array}{l} \frac{d^{2} y}{d x^{2}} = 12 x - 12 \\ Apabila x = 0, \frac{d^{2} y}{d x^{2}} = 12 (0) - 12 = - 12 < 0 \\ (0, - 6) adalah titik maksimum . \\ Apabila x = 2, \frac{d^{2} y}{d x^{2}} = 12 (2) - 12 = 12 > 0 \\ (2, - 14) adalah titik minimum . \end{array}

Soalan 4:

Rajah di bawah menunjukkan suatu lengkung x = y² – 1 yang bersilang dengan garis lurus 3y = 2x pada titik Q.

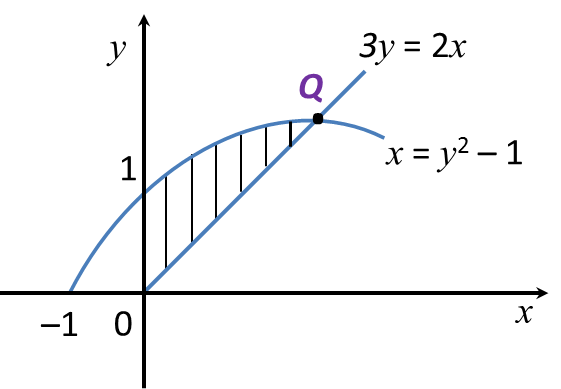
Hitungkan isipadu janaan apabila rantau berlorek itu dikisarkan melalui 360^opada paksi-y.

Penyelesaian:

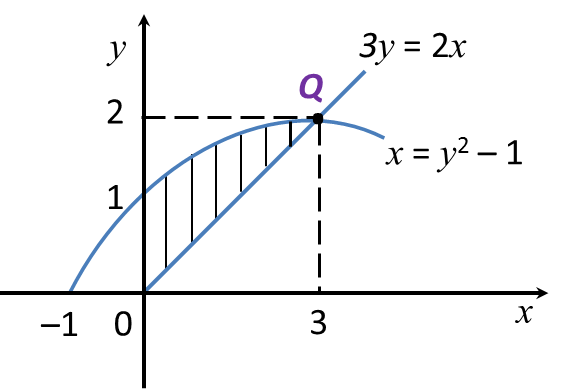
x = y² – 1 ---- (1)

3y = 2x

\begin{array}{l} x = \frac{3}{2} y \to (2) \\ Gantikan (2) ke dalam (1), \\ \frac{3}{2} y = y^{2} - 1 \end{array}

2y² – 3y – 2 = 0

(2y + 1) (y – 2) = 0

y = –½ atau y = 2

\begin{array}{l} apabila y = 2, x = \frac{3}{2} (2) = 3, Q = (3, 2) \\ I_{1} (Isipadu kon) \\ = \frac{1}{3} π r^{2} h = \frac{1}{3} π {(3)}^{2} (2) \\ = 6 π {unit}^{3} \end{array}

\begin{array}{l} I_{2} (Isipadu lengkung) \\ = π \int_{1}^{2} x^{2} d y \\ = π \int_{1}^{2} {(y^{2} - 1)}^{2} d y \\ = π \int_{1}^{2} (y^{4} - 2 y^{2} + 1) d y \\ = π {[\frac{y^{5}}{5} - \frac{2 y^{3}}{3} + y]}_{1}^{2} \\ = π [(\frac{2^{5}}{5} - \frac{2 {(2)}^{3}}{3} + 2) - (\frac{1^{5}}{5} - \frac{2 {(1)}^{3}}{3} + 1)] \\ = π (\frac{46}{15} - \frac{8}{15}) \\ = \frac{38}{15} π {unit}^{3} \end{array}

\begin{array}{l} Maka isipadu janaan = I_{1} - I_{2} \\ = 6 π - \frac{38}{15} π \\ = \frac{52}{15} π {unit}^{3} \end{array}