9.4.1 Penyelesaian Segitiga, SPM Praktis (Kertas 2)
Soalan 1:
Rajah di bawah menunjukkan sisi empat ABCD.
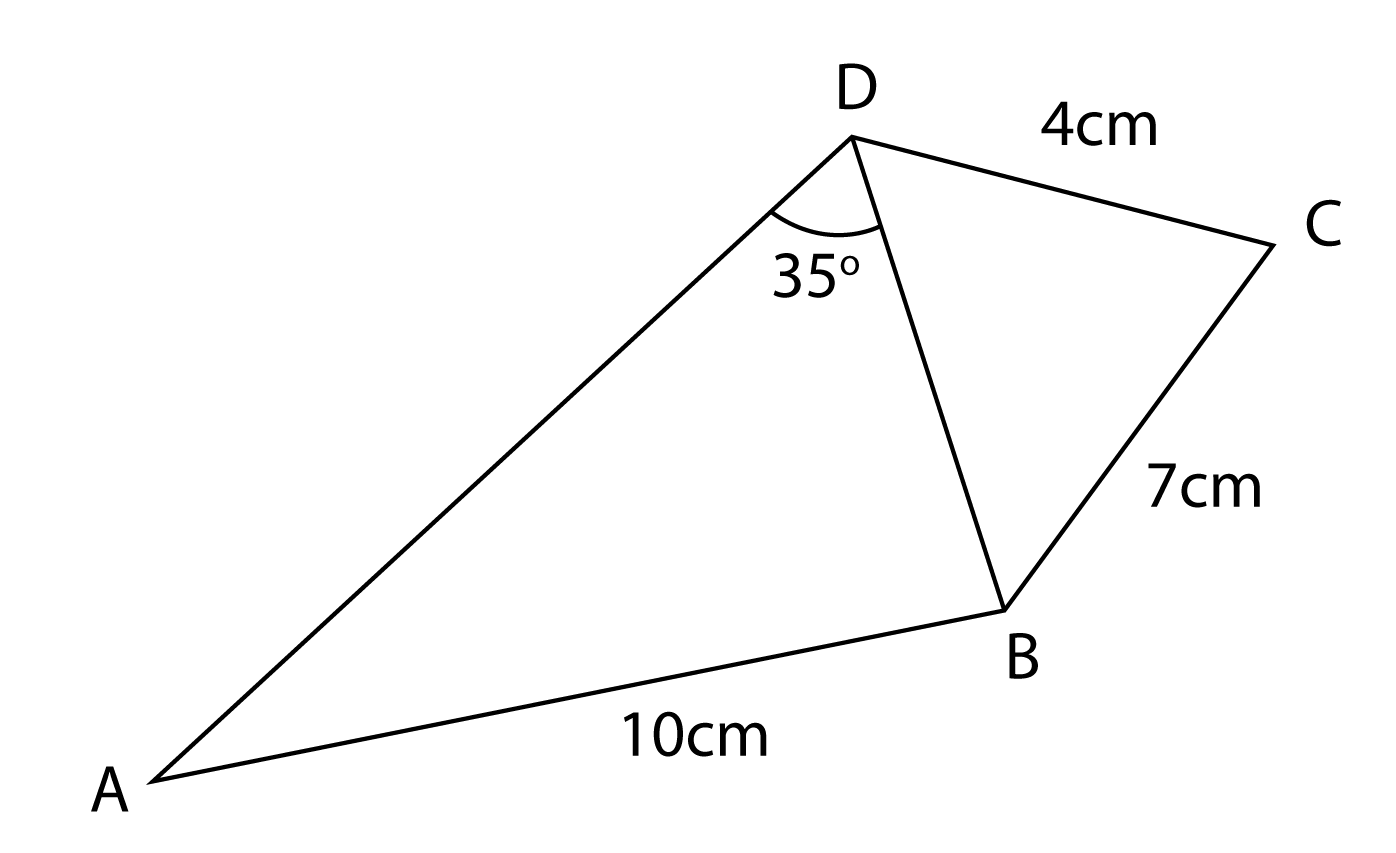

Luas segitiga BCD ialah 12 cm2 dan ∠BCD ialah tirus. Hitung
(a) ∠BCD,
(b) Panjang, dalam cm, bagi BD,
(c) ∠ABD,
(d) luas, dalam cm2, sisi empat ABCD.
Penyelesaian:
(a)
Diberi luas ∆ BCD = 12 cm2
½ (BC) (CD) sin C = 12
½ (7) (4) sin C= 12
14 sin C = 12
sin C = 12/14 = 0.8571
C = 59o
∠BCD = 59o
(b)
Guna petua kosinus,
BD2 = CD2 + BC2 – 2 (4)(7) kos 59o
BD2 = 42 + 72 – 2 (4)(7) kos 59o
BD2 = 65 – 28.84
BD2 = 36.16
BD = 6.013 cm
(c)
Guna petua sinus,
sin A = 0.3449
A = 20.18o
∠ABD = 180o– 35o – 20.18o
= 124.82o
(d)
Luas sisi empat ABCD
= Luas ∆ ABD + Luas ∆ BCD
= ½ (AB)(BD) sin B + 12 cm
= ½ (10) (6.013) sin 124.82 + 12
= 24.68 + 12
= 36.68 cm
Soalan 2:
Rajah di bawah menunjukkan trapezium ABCD.
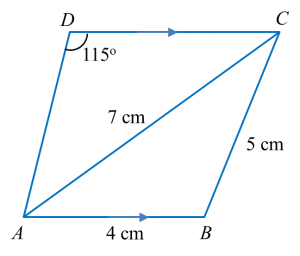 (a) Hitung
(a) Hitung
(i) ∠BAC.
(ii) panjang, dalam cm, bagi AD.
(b) Garis lurus AB dipanjangkan ke B’ dengan keadaan BC = B’C.
(i) Lakar trapezium AB’CD.
(ii) Hitung luas, dalam, cm2, bagi ∆BB’C.
Penyelesaian:
(a)(i)
(a)(ii)
(b)(i)
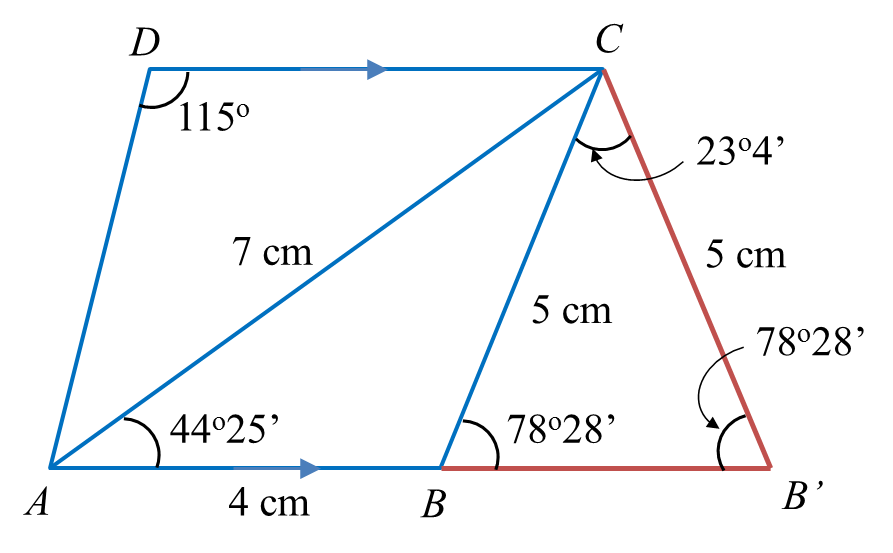
(b)(ii)
Rajah di bawah menunjukkan trapezium ABCD.
 (a) Hitung
(a) Hitung(i) ∠BAC.
(ii) panjang, dalam cm, bagi AD.
(b) Garis lurus AB dipanjangkan ke B’ dengan keadaan BC = B’C.
(i) Lakar trapezium AB’CD.
(ii) Hitung luas, dalam, cm2, bagi ∆BB’C.
Penyelesaian:
(a)(i)
(a)(ii)
(b)(i)

(b)(ii)