9.4.2 Penyelesaian Segitiga, SPM Praktis (Kertas 2)
Soalan 3:
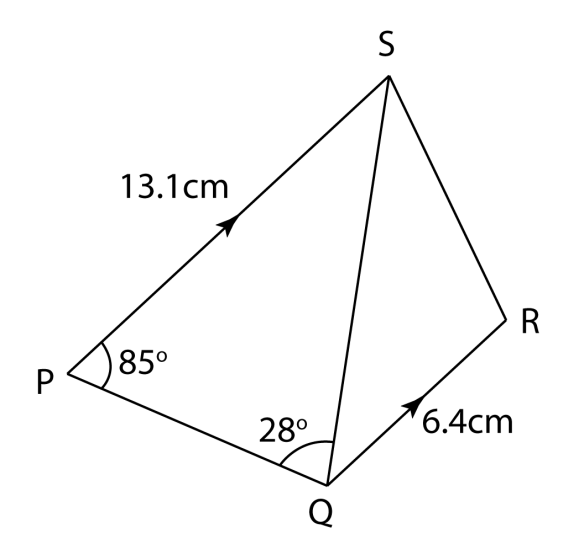
Rajah menunjukkan trapezium PQRS. PS adalah selari dengan QR dan ∠QRS ialah sudut cakah. Cari
(a) panjang, dalam cm, QS.
(b) panjang, dalam cm, RS.
(c) ∠QRS.
(d) luas, dalam cm2, segitiga QRS.
(a) panjang, dalam cm, QS.
(b) panjang, dalam cm, RS.
(c) ∠QRS.
(d) luas, dalam cm2, segitiga QRS.
Penyelesaian:
(a)
(b)
∠RQS = 180o– 85o – 28o
∠RQS = 67o
Guna petua kosinus,
RS2 = QR2+ QS2 – 2 (QR)(QS) kos ∠RQS
RS2 = 6.42 + 27.82 – 2 (6.4)(27.8) kos 67o
RS2 = 813.8 – 139.04
RS2 = 674.76
RS = 25.98 cm
(c)
Guna petua kosinus,
QS2 = QR2+ RS2 – 2 (QR)(RS) kos ∠RQS
27.82 = 6.42+ 25.982 – 2 (6.4)(25.98) kos∠QRS
772.84 = 715.92 – 332.54 kos∠QRS
kos∠QRS = –0.1712
∠QRS = 99.86o
(d)
Luas segitiga QRS
= ½ (QR)(RS) sin R
= ½ (6.4) (25.98) sin 99.86o
= 81.91 cm2
Soalan 4:
Rajah di bawah menunjukkan sebuah sisi empat PQRS.
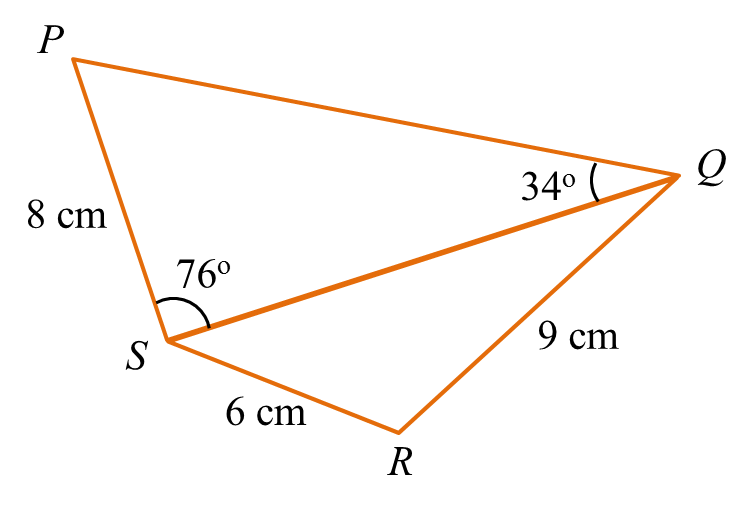
(a) Cari
(i) panjang, dalam cm, bagi QS.
(ii) ∠QRS.
(iii) luas, dalam cm2, bagi sisi empat PQRS.
(b)(i) Lakar sebuah segi tiga S’Q’R’ yang mempunyai bentuk berbeza daripada segi tiga SQR dengan keadaan S’R’ = SR, S’Q’ = SQ dan ∠S’Q’R’ = ∠SQR.
(ii) Seterusnya, nyatakan ∠S’R’Q’.
Penyelesaian:
(a)(i)
(a)(ii)
(a)(iii)
(b)(i)
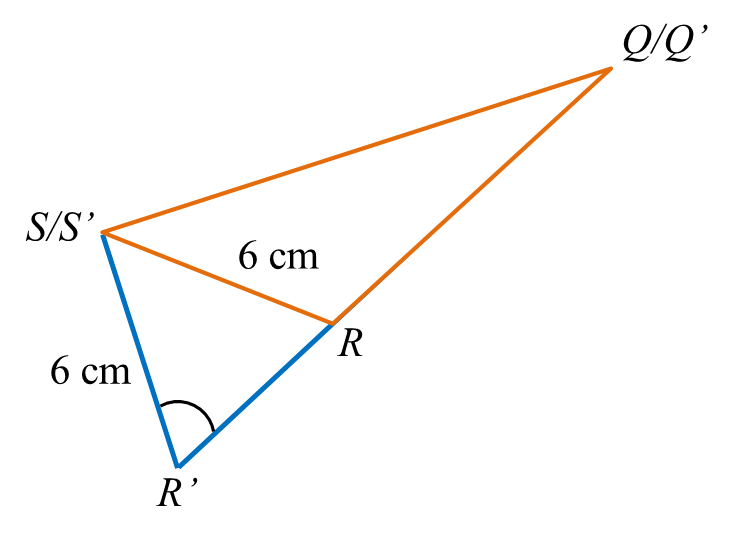
(b)(ii)
Rajah di bawah menunjukkan sebuah sisi empat PQRS.

(a) Cari
(i) panjang, dalam cm, bagi QS.
(ii) ∠QRS.
(iii) luas, dalam cm2, bagi sisi empat PQRS.
(b)(i) Lakar sebuah segi tiga S’Q’R’ yang mempunyai bentuk berbeza daripada segi tiga SQR dengan keadaan S’R’ = SR, S’Q’ = SQ dan ∠S’Q’R’ = ∠SQR.
(ii) Seterusnya, nyatakan ∠S’R’Q’.
Penyelesaian:
(a)(i)
(a)(ii)
(a)(iii)
(b)(i)

(b)(ii)