Soalan 9:
(a) Rajah 6 menunjukkan segi empat tepat ABCD.
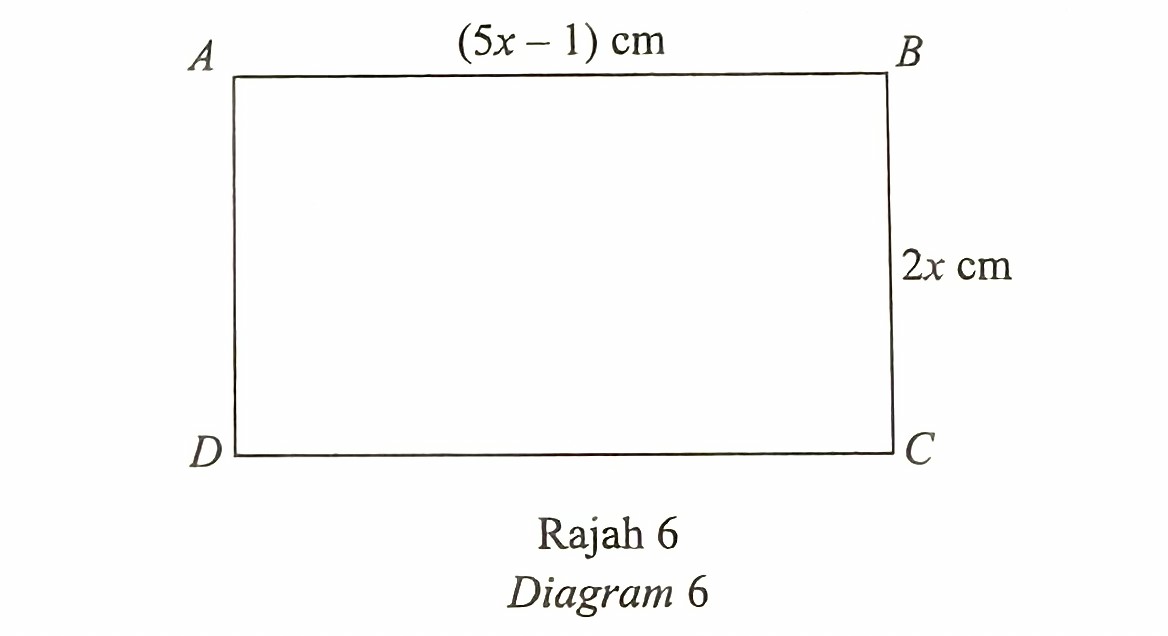
Pada suatu ketika, nilai x berubah dari 3 cm kepada (3 + p) cm, dengan keadaan p ialah suatu nilai kecil.
Menggunakan pembezaan, ungkapkan dalam sebutan p, perubahan kecil bagi luas ABCD, dalam cm2, pada ketika itu.
[3 markah]
(b) Rajah 7 menunjukkan dua lot petak tanah, P dan Q . Kedua-dua lot akan ditanam sepenuhnya dengan rumput yang sama jenis.
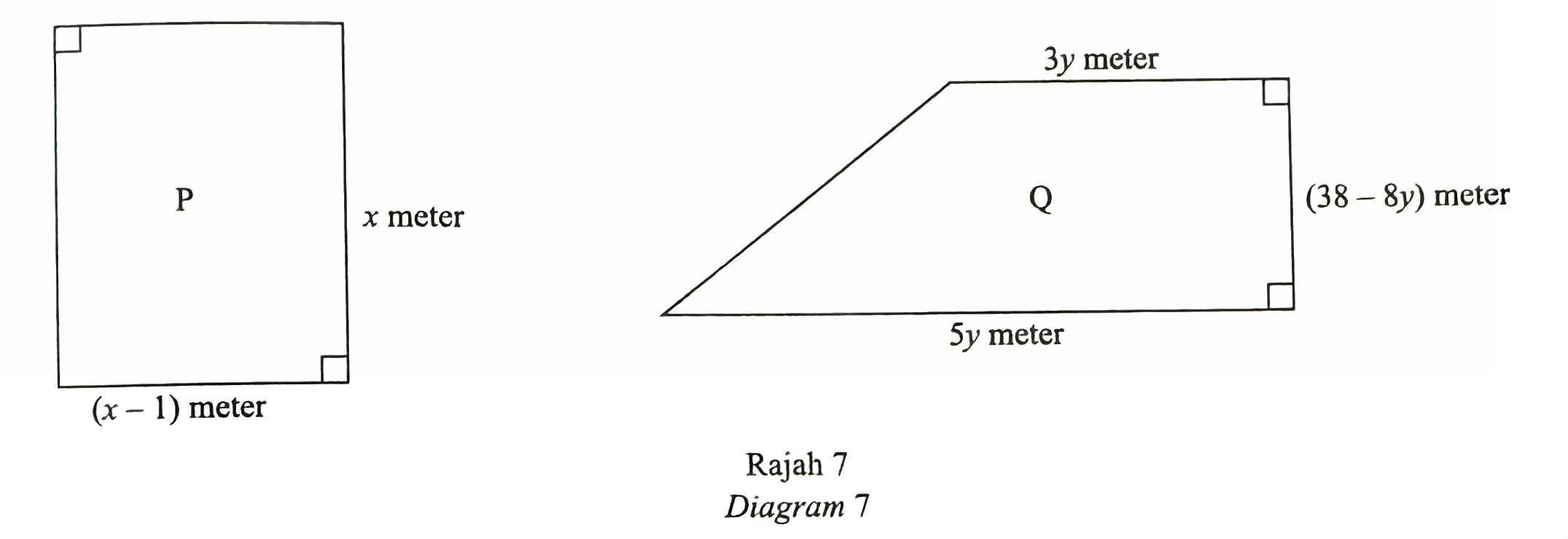
Diberi bahawa perimeter lot P ialah 54 m dan luas lot Q ialah L m2.
(i) Menggunakan pembezaan, cari nilai y, dengan keadaan L ialah maksimum.
(ii) Seterusnya, tentukan lot yang akan ditanam dengan rumput yang paling banyak. Justifikasikan jawapan anda.
[6 markah]
Jawapan:
(a)
$$ \begin{aligned} & Luas, A=2 x(5 x-1) \\ & A=10 x^2-2 x \end{aligned} $$
$$ \begin{aligned} & \frac{\mathrm{d} A}{\mathrm{~d} x}=20 x-2 \\ & \text { Apabila } x=3, \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=20(3)-2 \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=58 \end{aligned} $$
$$ \begin{aligned} & \frac{\delta A}{\delta x} \approx \frac{\mathrm{~d} A}{\mathrm{~d} x} \\ & \delta A=\frac{\mathrm{d} A}{\mathrm{~d} x} \times \delta x \\ & \delta A=(58)[(3+p)-3] \\ & \delta A=(58)(p) \\ & \delta A=58 p \end{aligned} $$
(b)(i)
$$ \begin{aligned} A & =\frac{1}{2}(3 y+5 y)(38-8 y) \\ & =\frac{1}{2}(8 y)(38-8 y) \\ & =4 y(38-8 y) \\ & =152 y-32 y^2 \end{aligned} $$
$$ \begin{aligned} \frac{\mathrm{d} A}{\mathrm{~d} y}: 152-64 y & =0 \\ -64 y & =-152 \\ y & =\frac{-152}{-64} \\ y & =2.375 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\frac{\mathrm{d}^2 A}{\mathrm{~d} y^2}=-64<0\\ &\therefore A \text { adalah maksimum apabila } y=2.375 \mathrm{~m} \text {. } \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \text { Luas } Q & =152 y-32 y^2 \\ & =152(2.375)-32(2.375)^2 \\ & =180.5 \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter, } P=54 \mathrm{~m}\\ &\begin{aligned} 2[(x-1)+x] & =54 \\ 2(2 x-1) & =54 \\ 2 x-1 & =27 \\ 2 x & =28 \\ x & =14 \mathrm{~m} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas } P & =(x-1)(x) \\ & =(14-1)(14) \\ & =182 \mathrm{~m}^2 \end{aligned} $$
Lot P yang akan ditanam dengan rumput yang paling banyak kerana luas P ialah 182 m2, iaitu 1.5 m2 lebih banyak daripada luas Q, iaitu 180.5 m2.
(a) Rajah 6 menunjukkan segi empat tepat ABCD.

Pada suatu ketika, nilai x berubah dari 3 cm kepada (3 + p) cm, dengan keadaan p ialah suatu nilai kecil.
Menggunakan pembezaan, ungkapkan dalam sebutan p, perubahan kecil bagi luas ABCD, dalam cm2, pada ketika itu.
[3 markah]
(b) Rajah 7 menunjukkan dua lot petak tanah, P dan Q . Kedua-dua lot akan ditanam sepenuhnya dengan rumput yang sama jenis.

Diberi bahawa perimeter lot P ialah 54 m dan luas lot Q ialah L m2.
(i) Menggunakan pembezaan, cari nilai y, dengan keadaan L ialah maksimum.
(ii) Seterusnya, tentukan lot yang akan ditanam dengan rumput yang paling banyak. Justifikasikan jawapan anda.
[6 markah]
Jawapan:
(a)
$$ \begin{aligned} & Luas, A=2 x(5 x-1) \\ & A=10 x^2-2 x \end{aligned} $$
$$ \begin{aligned} & \frac{\mathrm{d} A}{\mathrm{~d} x}=20 x-2 \\ & \text { Apabila } x=3, \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=20(3)-2 \\ & \frac{\mathrm{~d} A}{\mathrm{~d} x}=58 \end{aligned} $$
$$ \begin{aligned} & \frac{\delta A}{\delta x} \approx \frac{\mathrm{~d} A}{\mathrm{~d} x} \\ & \delta A=\frac{\mathrm{d} A}{\mathrm{~d} x} \times \delta x \\ & \delta A=(58)[(3+p)-3] \\ & \delta A=(58)(p) \\ & \delta A=58 p \end{aligned} $$
(b)(i)
$$ \begin{aligned} A & =\frac{1}{2}(3 y+5 y)(38-8 y) \\ & =\frac{1}{2}(8 y)(38-8 y) \\ & =4 y(38-8 y) \\ & =152 y-32 y^2 \end{aligned} $$
$$ \begin{aligned} \frac{\mathrm{d} A}{\mathrm{~d} y}: 152-64 y & =0 \\ -64 y & =-152 \\ y & =\frac{-152}{-64} \\ y & =2.375 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\frac{\mathrm{d}^2 A}{\mathrm{~d} y^2}=-64<0\\ &\therefore A \text { adalah maksimum apabila } y=2.375 \mathrm{~m} \text {. } \end{aligned} $$
(b)(ii)
$$ \begin{aligned} \text { Luas } Q & =152 y-32 y^2 \\ & =152(2.375)-32(2.375)^2 \\ & =180.5 \mathrm{~m}^2 \end{aligned} $$
$$ \begin{aligned} &\text { Perimeter, } P=54 \mathrm{~m}\\ &\begin{aligned} 2[(x-1)+x] & =54 \\ 2(2 x-1) & =54 \\ 2 x-1 & =27 \\ 2 x & =28 \\ x & =14 \mathrm{~m} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Luas } P & =(x-1)(x) \\ & =(14-1)(14) \\ & =182 \mathrm{~m}^2 \end{aligned} $$
Lot P yang akan ditanam dengan rumput yang paling banyak kerana luas P ialah 182 m2, iaitu 1.5 m2 lebih banyak daripada luas Q, iaitu 180.5 m2.