Soalan 7:
(a) Diberi bahawa tiga sebutan pertama bagi satu jujukan ialah 4, 8, 16.
(i) Nyatakan jenis jujukan. Beri satu sebab untuk jawapan anda.
(ii) Seterusnya, cari sebutan ke-n bagi jujukan itu.
[3 markah]
(b) Dalam suatu janjang aritmetik, sebutan ke-2 ialah 5p – 10 dan sebutan ke-10 adalah 7 kali sebutan pertama, a.
Ungkapkan a dalam sebutan p.
[3 markah]
(c) Sebuah poligon dengan n sisi dilukis dengan keadaan saiz sudut-sudut pedalamannya membentuk suatu janjang aritmetik. Diberi bahawa saiz sudut pedalaman terbesar adalah 5 kali saiz sudut pedalaman terkecil, a.
Ungkapkan a dalam sebutan n.
[2 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & 4,8,16 \\ & r_1=\frac{8}{4}=2 \\ & r_2=\frac{16}{8}=2 \end{aligned} $$
$$ \text { Janjang geometri kerana } r_1=r_2=2 $$
(a)(ii)
$$ \begin{aligned} T_n & =a r^n-1 \\ & =(4)(2)^{n-1} \\ & =\left(2^2\right)(2)^{n-1} \\ & =2^{n-1+2} \\ & =2^{n+1} \end{aligned} $$
(b)
$$ \begin{aligned} A P: T_n=a+ & (n-1) d \\ T_2 & =5 p-10 \\ a+(2-1) d & =5 p-10 \\ a+d & =5 p-10 \\ d & =5 p-10-a \ldots (1) \end{aligned} $$
$$ \begin{aligned} T_{10} & =7 a \\ a+(10-1) d & =7 a \\ a+9 d & =7 a \\ a+9(5 p-10-a) & =7 a \\ a+45 p-90-9 a) & =7 a \\ a-9 a-7 a & =90-45 p \\ -15 a & =90-45 p \\ a & =\frac{90-45 p}{-15} \\ a & =-6+3 p \end{aligned} $$
(c)
$$ T_1=a, T_n=5 a $$
$$ \begin{aligned} \text { Jumlah sudut } & =(n-2) \times 180^{\circ} \\ S_n & =(n-2) \times 180^{\circ} \\ \frac{n}{2}(a+l) & =(n-2) \times 180^{\circ} \\ \frac{n}{2}(a+5 a) & =(n-2) \times 180^{\circ} \\ \frac{n}{2}(6 a) & =(n-2) \times 180^{\circ} \\ 3 a n & =(n-2) \times 180^{\circ} \\ a & =\frac{(n-2) \times 180^{\circ}}{3 n} \\ a & =\frac{(n-2) \times 60^{\circ}}{n} \end{aligned} $$
(a) Diberi bahawa tiga sebutan pertama bagi satu jujukan ialah 4, 8, 16.
(i) Nyatakan jenis jujukan. Beri satu sebab untuk jawapan anda.
(ii) Seterusnya, cari sebutan ke-n bagi jujukan itu.
[3 markah]
(b) Dalam suatu janjang aritmetik, sebutan ke-2 ialah 5p – 10 dan sebutan ke-10 adalah 7 kali sebutan pertama, a.
Ungkapkan a dalam sebutan p.
[3 markah]
(c) Sebuah poligon dengan n sisi dilukis dengan keadaan saiz sudut-sudut pedalamannya membentuk suatu janjang aritmetik. Diberi bahawa saiz sudut pedalaman terbesar adalah 5 kali saiz sudut pedalaman terkecil, a.
Ungkapkan a dalam sebutan n.
[2 markah]
Jawapan:
(a)(i)
$$ \begin{aligned} & 4,8,16 \\ & r_1=\frac{8}{4}=2 \\ & r_2=\frac{16}{8}=2 \end{aligned} $$
$$ \text { Janjang geometri kerana } r_1=r_2=2 $$
(a)(ii)
$$ \begin{aligned} T_n & =a r^n-1 \\ & =(4)(2)^{n-1} \\ & =\left(2^2\right)(2)^{n-1} \\ & =2^{n-1+2} \\ & =2^{n+1} \end{aligned} $$
(b)
$$ \begin{aligned} A P: T_n=a+ & (n-1) d \\ T_2 & =5 p-10 \\ a+(2-1) d & =5 p-10 \\ a+d & =5 p-10 \\ d & =5 p-10-a \ldots (1) \end{aligned} $$
$$ \begin{aligned} T_{10} & =7 a \\ a+(10-1) d & =7 a \\ a+9 d & =7 a \\ a+9(5 p-10-a) & =7 a \\ a+45 p-90-9 a) & =7 a \\ a-9 a-7 a & =90-45 p \\ -15 a & =90-45 p \\ a & =\frac{90-45 p}{-15} \\ a & =-6+3 p \end{aligned} $$
(c)
$$ T_1=a, T_n=5 a $$
$$ \begin{aligned} \text { Jumlah sudut } & =(n-2) \times 180^{\circ} \\ S_n & =(n-2) \times 180^{\circ} \\ \frac{n}{2}(a+l) & =(n-2) \times 180^{\circ} \\ \frac{n}{2}(a+5 a) & =(n-2) \times 180^{\circ} \\ \frac{n}{2}(6 a) & =(n-2) \times 180^{\circ} \\ 3 a n & =(n-2) \times 180^{\circ} \\ a & =\frac{(n-2) \times 180^{\circ}}{3 n} \\ a & =\frac{(n-2) \times 60^{\circ}}{n} \end{aligned} $$
Soalan 8:
$$ \text { Diberi bahawa } \sin A=\frac{p}{2} \text { dan } \sin (A+B)-\sin (A-B)=2 p \text {, dengan keadaan } A \text { dan } B \text { ialah sudut tirus. } $$
Ungkapkan dalam sebutan p bagi
(a) kos A, [2 markah]
(b) sin B [3 markah]
Jawapan:
(a)
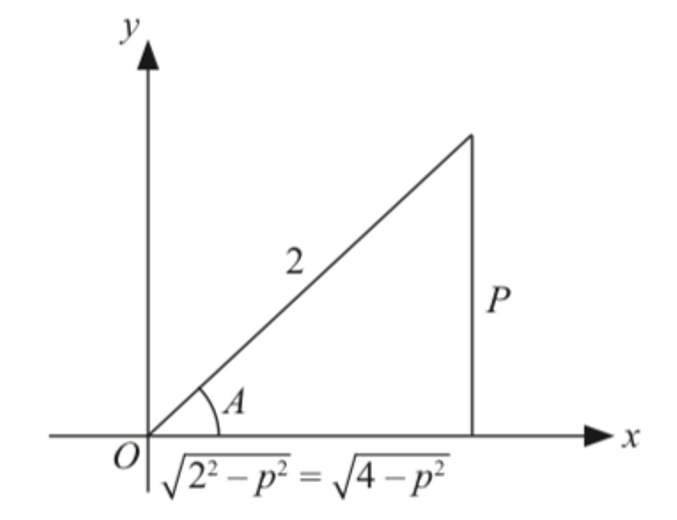
$$ \operatorname{kos} A=\frac{\sqrt{4-p^2}}{2} $$
(b)
$$ \begin{aligned} \sin (A+B)-\sin (A-B) & =2 p \\ (\sin A \operatorname{kos} B+\operatorname{kos} A \sin B)-(\sin A \operatorname{kos} B-\operatorname{kos} A \sin B) & =2 p \\ \sin A \operatorname{kos} B+\operatorname{kos} A \sin B-\sin A \operatorname{kos} B+\operatorname{kos} A \sin B & =2 p \\ 2 \operatorname{kos} A \sin B & =2 p \\ 2\left(\frac{\sqrt{4-p^2}}{2}\right) \sin B & =2 p \\ \sqrt{4-p^2} \sin B & =2 p \\ \sin B & =\frac{2 p}{\sqrt{4-p^2}} \end{aligned} $$
$$ \text { Diberi bahawa } \sin A=\frac{p}{2} \text { dan } \sin (A+B)-\sin (A-B)=2 p \text {, dengan keadaan } A \text { dan } B \text { ialah sudut tirus. } $$
Ungkapkan dalam sebutan p bagi
(a) kos A, [2 markah]
(b) sin B [3 markah]
Jawapan:
(a)

$$ \operatorname{kos} A=\frac{\sqrt{4-p^2}}{2} $$
(b)
$$ \begin{aligned} \sin (A+B)-\sin (A-B) & =2 p \\ (\sin A \operatorname{kos} B+\operatorname{kos} A \sin B)-(\sin A \operatorname{kos} B-\operatorname{kos} A \sin B) & =2 p \\ \sin A \operatorname{kos} B+\operatorname{kos} A \sin B-\sin A \operatorname{kos} B+\operatorname{kos} A \sin B & =2 p \\ 2 \operatorname{kos} A \sin B & =2 p \\ 2\left(\frac{\sqrt{4-p^2}}{2}\right) \sin B & =2 p \\ \sqrt{4-p^2} \sin B & =2 p \\ \sin B & =\frac{2 p}{\sqrt{4-p^2}} \end{aligned} $$