Soalan 9:
Given that
\(\sin\theta=\frac35\)
, dengan keadaan θ ialah sudut tirus, tanpa menggunakan jadual atau kalkulator, cari nilai bagi
(a) sin (180º + θ),
(b) kos (180º – θ),
(c) tan (360º + θ).
Penyelesaian:
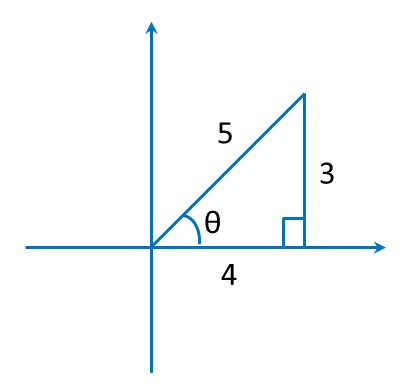

\(\sin\theta=\frac35\text{ }kos\theta=\frac45\text{ }\tan\theta=\frac34\)
sin (180º + θ)
= sin 180º kos θ + kos 180º sin θ
= (0) kos θ + (– 1) sin θ
= – sin θ
\(=-\frac35\)
(b)
kos (180º – θ)
= kos 180º kos θ + sin 180º sin θ
= (– 1) kos θ + (0) sin θ
= – kos θ
\(=-\frac45\)
(c)
\(\begin{array}{l}\tan{(360^\circ+\theta)}\\\\=\frac{\tan360^\circ+\tan\theta}{1-\tan360^\circ\tan\theta}\\\\=\frac{0+\tan\theta}{1-{(0)}{(\tan\theta)}}\\=\tan\theta\\=\frac34\end{array}\)
Soalan 10:
Buktikan setiap identiti trigonometri yang berikut.
(a) kot2 x – kot2 x kos2x = kos2 x
\(\text{(b)}\frac{\mathrm{sek}x}{\mathrm{sek}x-kosx}=kosek^2x\)
Penyelesaian:
(a)
Sebelah kiri:
kot2 x– kot2 x kos2 x
= kot2 x (1 – kos2 x)
= kot2 x (sin2 x)
\(\begin{array}{l}=\frac{kos^2x}{sin^2x}{(sin^2x)}\\=kos^2x\text{(Sebelah kanan)}\end{array}\)
(b)
\(\begin{array}{l}\text{Sebelah kiri:}\frac{\mathrm{sek}x}{\mathrm{sek}x-kosx}\\=\frac{\frac1{kosx}}{\frac1{kosx}-kosx}=\frac{\frac1{kosx}}{\frac1{kosx}-\frac{kos^2x}{kosx}}\\=\frac{\frac1{kosx}}{\frac{1-kos^2x}{kosx}}=\frac1{kosx}\times\frac{kosx}{1-kos^2x}\\=\frac1{1-kos^2x}=\frac1{sin^2x}\\=kosek^2x\text{(Sebelah kanan)}\end{array}\)