Soalan 7:
Diberi bahawa
\(\sin A=\frac5{13}\text{ dan kos}B=\frac45\)
, dengan keadaan A ialah sudut cakah dan B ialah
sudut tirus. Cari
(a) tan A
(b) sin (A + B)
(c) kos (A – B)
Penyelesaian:

\(\tan A=-\frac5{12}\)
(b)
\(\begin{array}{l}\sin{(A+B)}=\sin AkosB+kosA\sin B\\\sin{(A+B)}\\={(\frac5{13})}{(\frac45)}+{(-\frac{12}{13})}{(\frac35)}\leftarrow\boxed{\begin{array}{l}kosA=-\frac{12}{13}\\\sin B=\frac35\end{array}}\\=\frac4{13}-\frac{36}{65}\\=-\frac{16}{65}\end{array}\)
Soalan 8:
Jika sin A = p, dan 90° < A < 180°, ungkap dalam sebutan p
(a) tan A
(b) cos A
(c) sin 2A
Penyelesaian:
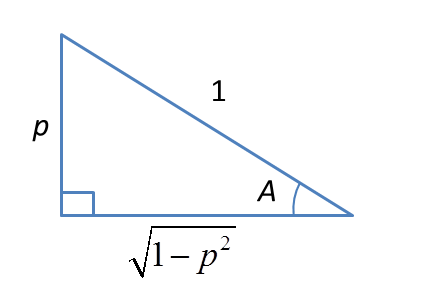

\(\begin{array}{l}\text{Guna Teori Pythagoras,}\\\text{Sisi bersebelahan}\\=\sqrt{1^2-p^2}\\=\sqrt{1-p^2}\end{array}\)
\(\tan A=-\frac p{\sqrt{1-p^2}}\leftarrow\boxed{\begin{array}{l}\text{tan bernilai negatif}\\\text{di sukuan II}\end{array}}\)
(b)
\(\begin{array}{l}kosA=-\sqrt{1-p^2}\leftarrow\boxed{\begin{array}{l}kos\text{ bernilai negatif di}\\\text{sukuan II}\end{array}}\\\sin A=2\sin AkosA\\\sin A=2{(p)}{(-\sqrt{1-p^2})}\\\sin A=-2p\sqrt{1-p^2}\end{array}\)
(c)
\(\begin{array}{l}\sin A=2\sin AkosA\\\sin A=2{(p)}{(-\sqrt{1-p^2})}\\\sin A=-2p\sqrt{1-p^2}\end{array}\)