8.4 Pengungkapan Suatu Vektor sebagai Gabungan Linear Vektor yang lain

8.4 Pengungkapan Suatu Vektor sebagai Gabungan Linear Vektor yang lain

1. Hukum Poligon Vektor

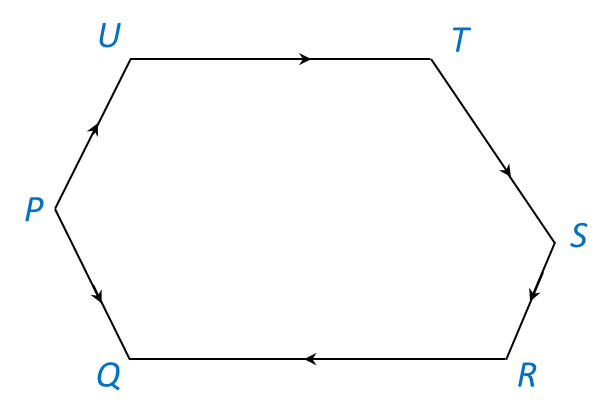
\vec{P Q} = \vec{P U} + \vec{U T} + \vec{T S} + \vec{S R} + \vec{R Q}

2. Untuk membuktikan dua vector adalah selari, kita mesti mengungkapkan salah satu vector sebagai kuantiti scalar kepada vector yang lain.

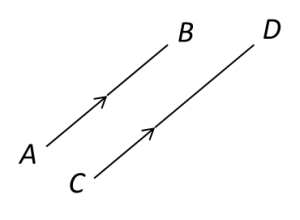
Misalnya,

\vec{A B} = k \vec{C D} atau \vec{C D} = h \vec{A B} .

3. Untuk membuktikan titik P, Q dan R adalah segaris, buktikan salah satu daripada berikut:

\begin{array}{l} • \vec{P Q} = k \vec{Q R} atau \vec{Q R} = h \vec{P Q} \\ • \vec{P R} = k \vec{P Q} atau \vec{P Q} = h \vec{P R} \\ • \vec{P R} = k \vec{Q R} atau \vec{Q R} = h \vec{P R} \end{array}

Contoh:

Rajah di bawah menunjukkan sebuah segiempat selari ABCD. Titik Q terletak pada garis lurus AB dan titik S terletak pada garis lurus DC. Garis lurus AS dipanjangkan ke titik T dengan keadaan AS = 2ST.

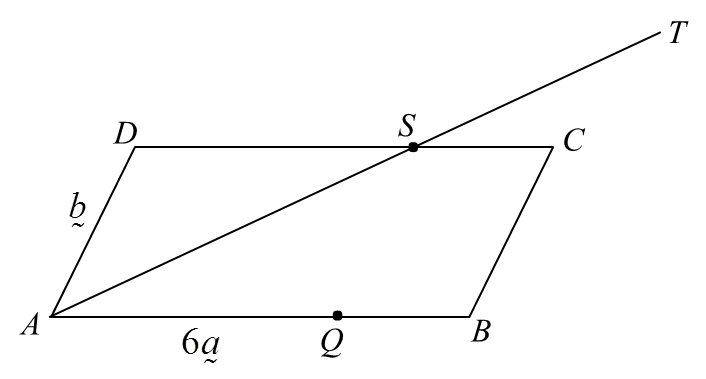
Diberi bahawa AQ : QB = 3 : 1, DS : SC = 3 : 1,

\vec{A Q} = 6 \underset{˜}{a} dan \vec{A D} = \underset{˜}{b}

(a) Ungkapan dalam sebutan

\underset{˜}{a} dan \underset{˜}{b} :

(i) \vec{A S} (ii) \vec{Q C}

(b) Seterusnya, tunjukkan titik Q, C dan T adalah segaris.

Penyelesaian:

(a)(i)

\begin{array}{l} \vec{A S} = \vec{A D} + \vec{D S} \\ = \vec{A D} + \vec{A Q} \leftarrow \begin{array}{l} A Q : Q B = 3 : 1 dan \\ D S : S C = 3 : 1 \\ ∴ \vec{A Q} = \vec{D S} \end{array} \\ = \underset{˜}{b} + 6 \underset{˜}{a} \\ = 6 \underset{˜}{a} + \underset{˜}{b} \end{array}

(a)(ii)

\begin{array}{l} \vec{Q C} = \vec{Q B} + \vec{B C} \\ = \frac{1}{3} \vec{A Q} + \vec{A D} \leftarrow \begin{array}{l} A Q : Q B = 3 : 1 \\ \frac{A Q}{Q B} = \frac{3}{1} \Rightarrow Q B = \frac{1}{3} A Q \\ bagi segiempat selari, \\ B C / / A D, B C = A D \end{array} \\ = \frac{1}{3} (6 \underset{˜}{a}) + \underset{˜}{b} \\ = 2 \underset{˜}{a} + \underset{˜}{b} \end{array}

(b)

\begin{array}{l} \vec{Q T} = \vec{Q A} + \vec{A T} \\ = \vec{Q A} + \frac{3}{2} \vec{A S} \leftarrow \begin{array}{l} A S = 2 S T \\ A T = 3 S T = \frac{3}{2} A S \end{array} \\ = - 6 \underset{˜}{a} + \frac{3}{2} (6 \underset{˜}{a} + \underset{˜}{b}) \\ = 3 \underset{˜}{a} + \frac{3}{2} \underset{˜}{b} \\ = \frac{3}{2} (2 \underset{˜}{a} + \underset{˜}{b}) \\ = \frac{3}{2} \vec{Q C} \\ Maka Q, C dan T adalah segaris . \end{array}

Leave a Comment Cancel reply