1.2.1 Fungsi
(A) Fungsi Sebagai Sejenis Hubungan Khas
1. Dalam sesuatu fungsi, semua objek dalam domain mesti dipadankan dengan hanya satu unsur dalam kodomain. Tetapi, semua unsur dalam kodomain tidak semestinya dipadankan dengan unsur dalam domain.
2. Fungsi ialah hubungan khas dengan setiap objek dalam domain mempunyai hanya satu imej. Bukan semua hubungan ialah fungsi.
3. Hubungan satu kepada satu dan hubungan banyak kepada satu ialah fungsi.
Contoh:
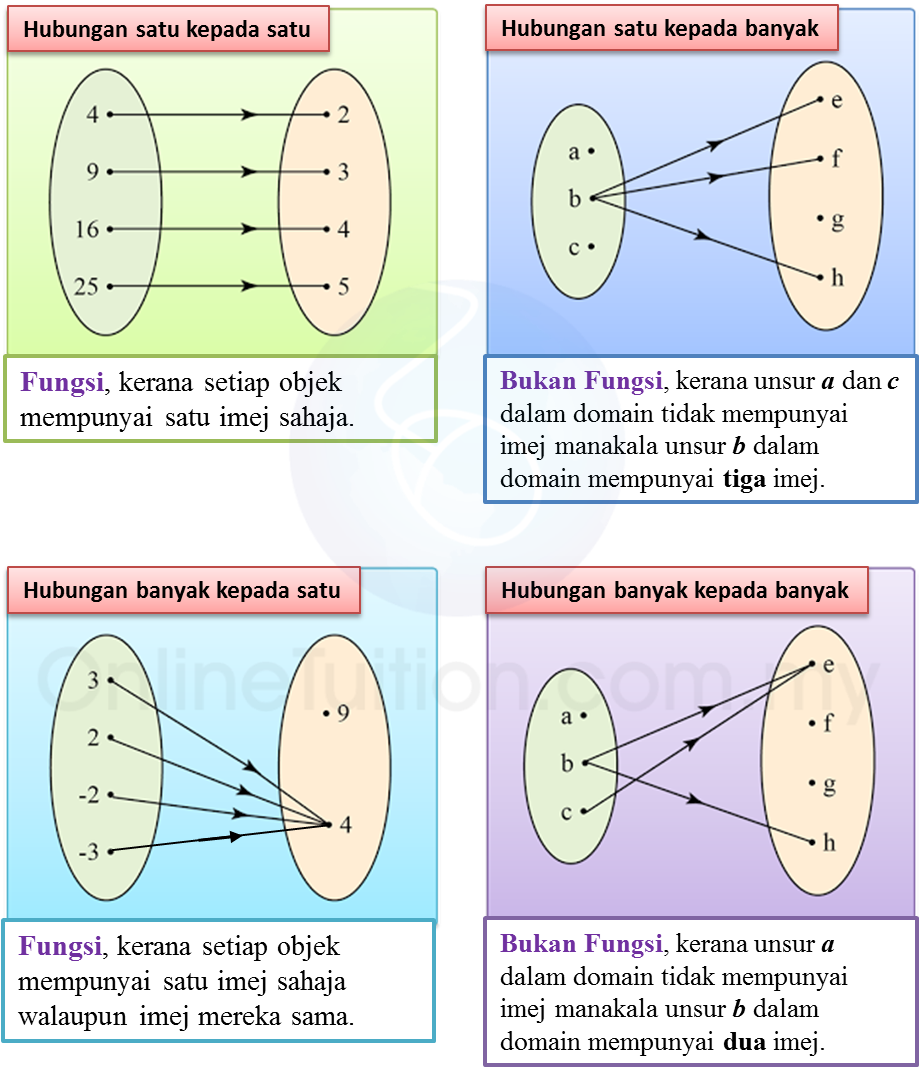

(B) Tatatanda Fungsi
Dalam tatatanda fungsi, sesuatu fungsi boleh diwakili oleh huruf abjad seperti f, g, h dan sebagainya. Misalnya, fungsi f yang memetakan objek x dalam domain kepada imej y dalam julat doleh ditulis sebagai
f : x → y atau f (x) = y
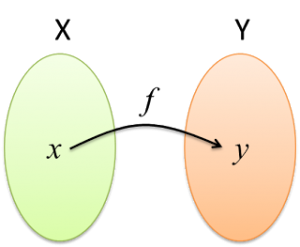

Seperti yang ditunjukkan dalam rajah di atas, fungsi f : X → Y, setiap unsur x dalam domain X mempunyai satu imej yang unik dalam kodomain Y.
Contoh 1:
Diberi fungsi f : x → 5x + 1, cari nilai bagi
(a) f (2)
(b) f (–3)
\(\text{(c) } f \left(\right. \frac{2}{5} \left.\right)\)
Penyelesaian:
(a)
f (x) = 5x + 1
f (2) = 5(2) + 1 = 11
(b)
f (x) = 5x + 1
f (–3) = 5 (–3) + 1 = –14
(c)
f (x) = 5x + 1
\(f \left(\right. \frac{2}{5} \left.\right) = 5 \left(\right. \frac{2}{5} \left.\right) + 1 = 3\)
Contoh 2:
Suatu fungsi x ditakrifkan sebagai
\(f : x \rightarrow \frac{5}{2 x - 1} , x \neq k .\)
Cari nilai k.
Penyelesaian:
\(\begin{array}{l}f{(x)}=\frac5{2x-1},\text{ }x\neq k\\\Rightarrow f{(x)}\text{ tidak tertakrif apabila }2x-1=0\\\text{oleh itu, }2x-1\neq0\\\text{ }2x\neq1\\\text{ }x\neq\frac12\\\text{Maka }k=\frac12\end{array}\)
f(x) tidak tertakrif apabila 2x-1=0
Apa maksud ni?
Maksudnya 2x-1 pada penyebut tidak boleh jadi 0.
Kalau nilai dia 0, nanti akan jadi 5/0, iaitu tak valid