Soalan 13:
Penyelesaian secara lakaran graf tidak diterima.
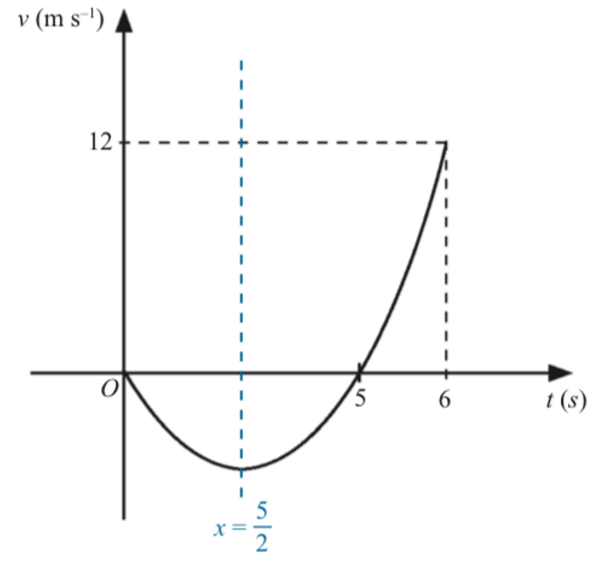
Suatu zarah bergerak di sepanjang suatu garis lurus dari satu titik tetap O. Rajah 7 menunjukkan graf halaju-masa bagi gerakan zarah itu.
[Anggapkan gerakan ke arah kanan sebagai positif]
 (a) Nyatakan
(a) Nyatakan
(i) masa, dalam saat, ketika zarah itu berhenti seketika,
(ii) julat masa, dalam saat, apabila zarah itu bergerak ke arah kiri.
[2 markah]
(b) Diberi bahawa graf halaju-masa itu ialah suatu fungsi kuadratik.
(i) Tunjukkan bahawa v = 2t2 – 10t.
(ii) Cari pecutan, dalam m s-2, apabila t = 2 saat.
(iii) Cari jarak, dalam m, yang dilalui oleh zarah itu dari p saat hingga saat ke-6, dengan keadaan p ialah masa ketika mencapai halaju maksimum sebelum ia bertukar arah.
[8 markah]
Jawapan:
(a)(i) t = 5 s
(a)(ii) Bergerak ke kiri: v < 0, 0 < t < 5
(b)(i)
$$ \begin{aligned} & v=a t^2+b t+c \text { pada } (0,0) \\ & 0=a(0)^2+b(0)+c \\ & 0=c \end{aligned} $$
$$ \begin{aligned} v & =a t^2+b t+c \text { pada } (5,0) \\ 0 & =a(5)^2+b(5)+c \\ 0 & =25 a+5 b \\ -25 a & =5 b \\ -5 a & =b \end{aligned} $$
$$ \begin{aligned} v & =a t^2+b t+c \text { pada } (6,12) \\ 12 & =a(6)^2+b(6) \\ 12 & =36 a+6(-5 a) \\ 12 & =36 a-30 a \\ 12 & =6 a \\ 2 & =a \end{aligned} $$
$$ \begin{aligned} & \text { Dari (1), } b=-5(2) \\ & =-10 \\ & \therefore v=2 t^2-10(\text { Tertunjuk }) \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & v=2 t^2-10 \\ & a=\frac{d V}{d t} \\ & a=4 t-10 \text { apabila } t=2 \mathrm{~s} \\ & a=4(2)-10 \\ & a=-2 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(b)(iii)
$$ \begin{aligned} &\text { Halaju maksimum : } a=0\\ &\begin{aligned} 4 t-10 & =0 \\ 4 t & =10 \\ t & =\frac{5}{2} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Jarak } \\ & =\left|\int_{\frac{5}{2}}^5\left(2 t^2-10 t\right) \mathrm{dt}\right|+\int_5^6\left(2 t^2-10 t\right) \mathrm{dt} \\ & =\left|\left[\frac{2}{3} t^3-5 t^2\right]_{\frac{5}{2}}^5\right|+\left[\frac{2}{3} t^3-5 t^2\right]_5^6 \\ & =\left|\left[\frac{2}{3}(5)^3-5(5)^2\right]-\left|\left[\frac{2}{3}\left(\frac{5}{2}\right)^3-5\left(\frac{5}{2}\right)^2\right]\right|+\left\{\left[\frac{2}{3}(6)^3-5(6)^2\right]-\right.\right. \\ & \left.\left[\frac{2}{3}(5)^3-5(5)^2\right]\right\} \\ & =\left|-\frac{125}{3}-\left(-\frac{125}{6}\right)\right|+\left[-36-\left(-\frac{125}{3}\right)\right] \\ & =\left|-\frac{125}{6}\right|+\frac{17}{3} \\ & =\frac{125}{6}+\frac{17}{3} \\ & =26 \frac{1}{2} \mathrm{~m} \end{aligned} $$
Penyelesaian secara lakaran graf tidak diterima.
Suatu zarah bergerak di sepanjang suatu garis lurus dari satu titik tetap O. Rajah 7 menunjukkan graf halaju-masa bagi gerakan zarah itu.
[Anggapkan gerakan ke arah kanan sebagai positif]
 (a) Nyatakan
(a) Nyatakan(i) masa, dalam saat, ketika zarah itu berhenti seketika,
(ii) julat masa, dalam saat, apabila zarah itu bergerak ke arah kiri.
[2 markah]
(b) Diberi bahawa graf halaju-masa itu ialah suatu fungsi kuadratik.
(i) Tunjukkan bahawa v = 2t2 – 10t.
(ii) Cari pecutan, dalam m s-2, apabila t = 2 saat.
(iii) Cari jarak, dalam m, yang dilalui oleh zarah itu dari p saat hingga saat ke-6, dengan keadaan p ialah masa ketika mencapai halaju maksimum sebelum ia bertukar arah.
[8 markah]
Jawapan:
(a)(i) t = 5 s
(a)(ii) Bergerak ke kiri: v < 0, 0 < t < 5
(b)(i)

$$ \begin{aligned} & v=a t^2+b t+c \text { pada } (0,0) \\ & 0=a(0)^2+b(0)+c \\ & 0=c \end{aligned} $$
$$ \begin{aligned} v & =a t^2+b t+c \text { pada } (5,0) \\ 0 & =a(5)^2+b(5)+c \\ 0 & =25 a+5 b \\ -25 a & =5 b \\ -5 a & =b \end{aligned} $$
$$ \begin{aligned} v & =a t^2+b t+c \text { pada } (6,12) \\ 12 & =a(6)^2+b(6) \\ 12 & =36 a+6(-5 a) \\ 12 & =36 a-30 a \\ 12 & =6 a \\ 2 & =a \end{aligned} $$
$$ \begin{aligned} & \text { Dari (1), } b=-5(2) \\ & =-10 \\ & \therefore v=2 t^2-10(\text { Tertunjuk }) \end{aligned} $$
(b)(ii)
$$ \begin{aligned} & v=2 t^2-10 \\ & a=\frac{d V}{d t} \\ & a=4 t-10 \text { apabila } t=2 \mathrm{~s} \\ & a=4(2)-10 \\ & a=-2 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(b)(iii)
$$ \begin{aligned} &\text { Halaju maksimum : } a=0\\ &\begin{aligned} 4 t-10 & =0 \\ 4 t & =10 \\ t & =\frac{5}{2} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Jarak } \\ & =\left|\int_{\frac{5}{2}}^5\left(2 t^2-10 t\right) \mathrm{dt}\right|+\int_5^6\left(2 t^2-10 t\right) \mathrm{dt} \\ & =\left|\left[\frac{2}{3} t^3-5 t^2\right]_{\frac{5}{2}}^5\right|+\left[\frac{2}{3} t^3-5 t^2\right]_5^6 \\ & =\left|\left[\frac{2}{3}(5)^3-5(5)^2\right]-\left|\left[\frac{2}{3}\left(\frac{5}{2}\right)^3-5\left(\frac{5}{2}\right)^2\right]\right|+\left\{\left[\frac{2}{3}(6)^3-5(6)^2\right]-\right.\right. \\ & \left.\left[\frac{2}{3}(5)^3-5(5)^2\right]\right\} \\ & =\left|-\frac{125}{3}-\left(-\frac{125}{6}\right)\right|+\left[-36-\left(-\frac{125}{3}\right)\right] \\ & =\left|-\frac{125}{6}\right|+\frac{17}{3} \\ & =\frac{125}{6}+\frac{17}{3} \\ & =26 \frac{1}{2} \mathrm{~m} \end{aligned} $$