Soalan 23 (4 markah):
Satu set data terdiri daripada 2, 3, 4, 5 dan 6. Setiap nombor didarab dengan m dan ditambah dengan n, dengan keadaan m dan n adalah integer. Diberi bahawa min baharu ialah 17 dan sisihan piawai baharu ialah 4.242.
Cari nilai m dan nilai n.
Penyelesaian:
Satu set data terdiri daripada 2, 3, 4, 5 dan 6. Setiap nombor didarab dengan m dan ditambah dengan n, dengan keadaan m dan n adalah integer. Diberi bahawa min baharu ialah 17 dan sisihan piawai baharu ialah 4.242.
Cari nilai m dan nilai n.
Penyelesaian:
Soalan 24 (3 markah):
Rajah 9 menunjukkan graf bagi taburan binomial X ~ B(3, p).
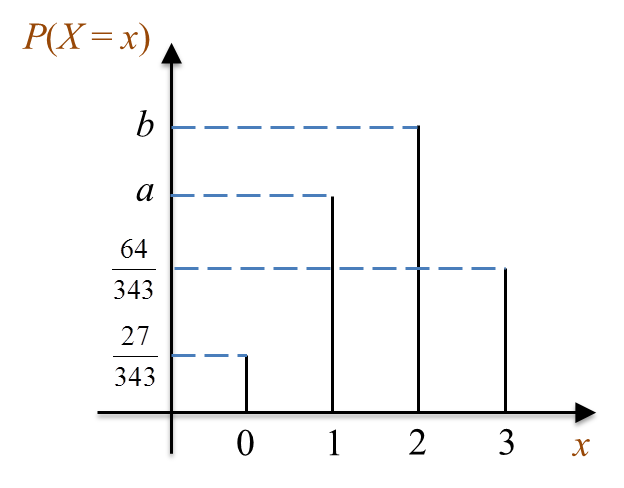 Rajah 9
Rajah 9
(a) Ungkapkan P(X = 0) + P(X > 2) dalam sebutan a dan b.
(b) Cari nilai p.
Penyelesaian:
(a)
P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 1
P(X = 0) + a + b + P(X = 3) = 1
P(X = 0) + P(X = 3) = 1 – a – b
P(X = 0) + P(X > 2) = 1 – a – b
(b)
Rajah 9 menunjukkan graf bagi taburan binomial X ~ B(3, p).
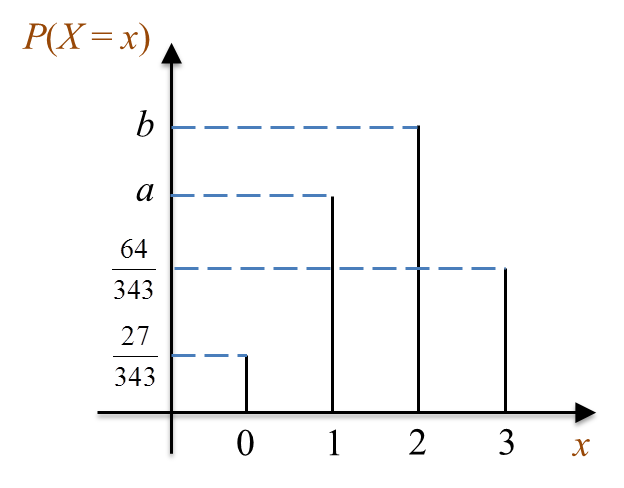 Rajah 9
Rajah 9(a) Ungkapkan P(X = 0) + P(X > 2) dalam sebutan a dan b.
(b) Cari nilai p.
Penyelesaian:
(a)
P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) = 1
P(X = 0) + a + b + P(X = 3) = 1
P(X = 0) + P(X = 3) = 1 – a – b
P(X = 0) + P(X > 2) = 1 – a – b
(b)
Soalan 25 (4 markah):
Rajah 10 menunjukkan satu graf taburan normal piawai.
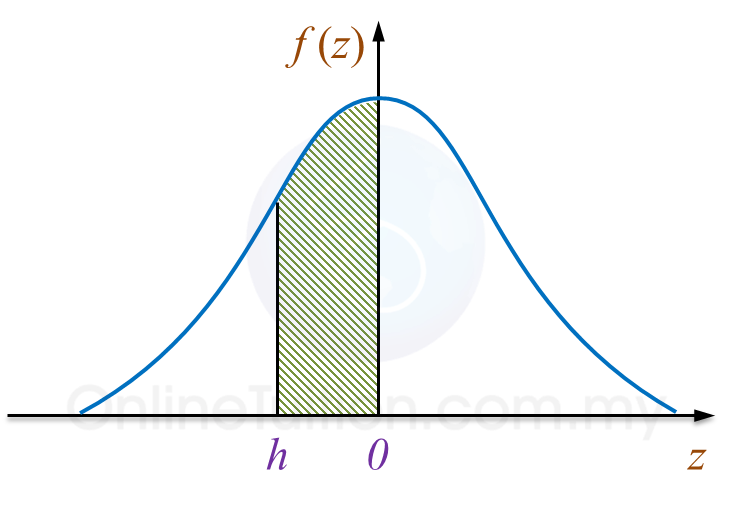 Rajah 10
Rajah 10
Kebarangkalian yang diwakili oleh luas kawasan berlorek ialah 0.2881.
(a) Cari nilai h.
(b) X ialah pemboleh ubah rawak selanjar bertaburan secara normal dengan min, μ dan varians 16.
Cari nilai μ jika skor-z bagi X = 58.8 ialah h.
Penyelesaian:
(a)
P(X < h) = 0.5 – 0.2881
P(X < h) = 0.2119
P(X < –0.8) = 0.2119
h = –0.8
(b)
Rajah 10 menunjukkan satu graf taburan normal piawai.
 Rajah 10
Rajah 10Kebarangkalian yang diwakili oleh luas kawasan berlorek ialah 0.2881.
(a) Cari nilai h.
(b) X ialah pemboleh ubah rawak selanjar bertaburan secara normal dengan min, μ dan varians 16.
Cari nilai μ jika skor-z bagi X = 58.8 ialah h.
Penyelesaian:
(a)
P(X < h) = 0.5 – 0.2881
P(X < h) = 0.2119
P(X < –0.8) = 0.2119
h = –0.8
(b)