1.3a Fungsi Gubahan
|
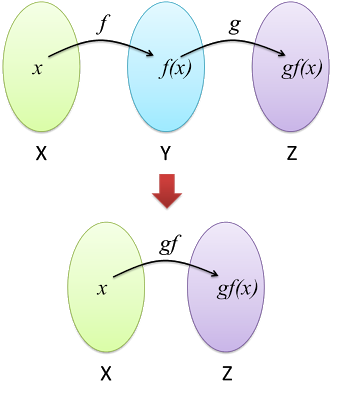
Jika fungsi f : X → Y,
dan fungsi g : Y → Z,
maka, fungsi gubahan gf: X → Z
|
Soalan 1:
Diberi fungsi f : x → 2x + 5 dan g : x→ x2 – 1, cari gf (2)
Penyelesaian:
f (x) = 2x + 5
f (2) = 2(2) + 5 = 9
gf (2) = g [f (2)] = g (9)
g(x) = x2– 1
gf(2) = g(9) = 92 – 1 = 80
Soalan 2:
Jika f : x → x + 5 dan g : x → x2 + 2x + 3, cari
(a) nilai gf (2),
(b) nilai fg (2 ),
(c) fungsi gubahanfg,
(d) fungsi gubahan gf,
(e) fungsi gubahan g2,
(f) fungsi gubahan f 2.
Penyelesaian:


Pembetulan bagi (c)
 Pembetulan bagi (e)
Pembetulan bagi (e)
Jawapan (e) btl ke?
Thanks for pointing our mistake.
We have done the correction accordingly.