6.8.1 Fungsi Trigonometri, SPM Praktis (Kertas 2)
Soalan 1:
(a) Lakar graf y = kos 2x untuk 0o ≤ x ≤ 180o.
(b) Seterusnya, dengan menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk mencari bilangan penyelesaian bagi persamaan
\(2\text{ sin}^2x=2-\frac x{180}\)
untuk 0o ≤ x ≤ 180o.
Nyatakan bilangan penyelesaian itu.
Penyelesaian:
(a)(b)
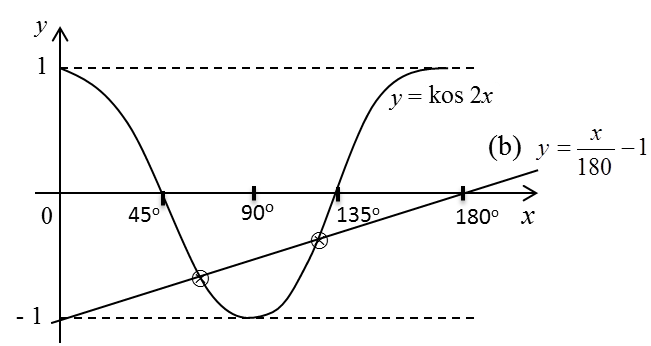
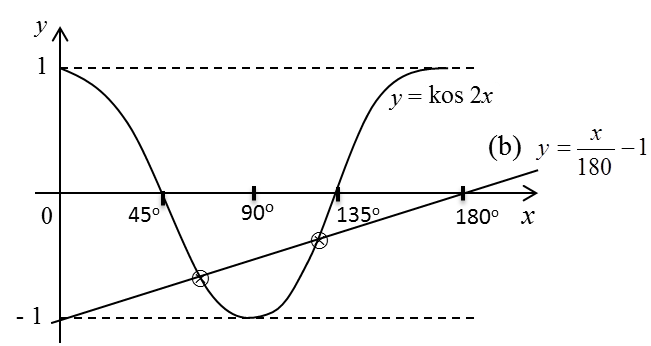
(b)
\(\begin{array}{l}2\text{ sin}^2x=2-\frac x{180}\\1-2\text{ sin}^2x=1-{(2-\frac x{180})}\\kos2x=\frac x{180}-1\\y=\frac x{180}-1\end{array}\)
x = 0, y = –1
x = 180, y = 0
Bilangan penyelesaian = 2
Soalan 2:
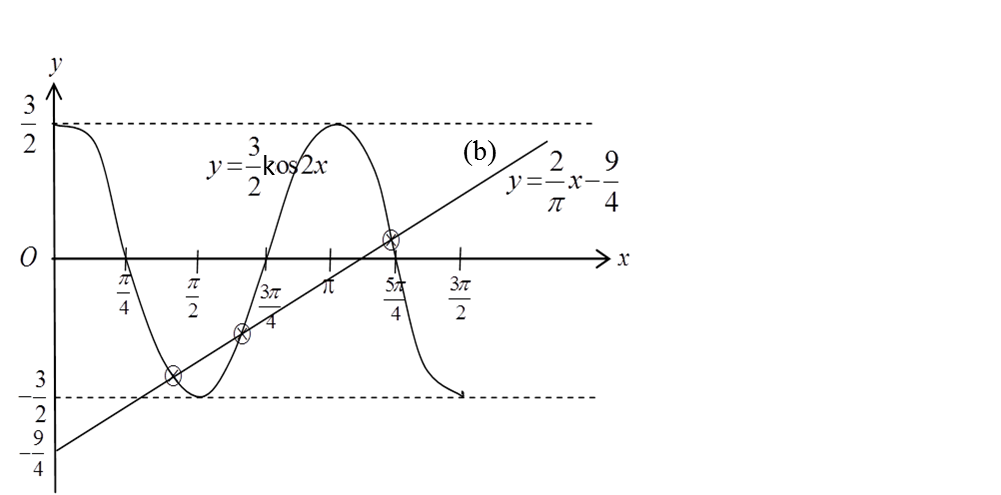
(a) Lakar graf
\(y=\frac32kos2x\text{ untuk }0\leq x\leq\frac32\pi.\)
(b) Seterusnya, dengan menggunakan paksi yang sama, lakar satu garis lurus yang sesuai untuk mencari bilangan penyelesaian bagi persamaan
\(\frac4{3\pi}x-kos2x=\frac32\text{ untuk }0\leq x\leq\frac32\pi\)
Nyatakan bilangan penyelesaian itu.
Penyelesaian:
(a)(b)

(b)
\(\begin{array}{l}\frac4{3\pi}x-kos2x=\frac32\\kos2x=\frac4{3\pi}x-\frac32\\\frac32kos2x=\frac32{(\frac4{3\pi}x-\frac32)}\\y=\frac2\pi x-\frac94\\\\\text{Untuk melakar graf }y=\frac2\pi x-\frac94\\x=0,\text{ }y=-\frac94\\x=\frac{3\pi}2,\text{ }y=\frac34\end{array}\)
Bilangan penyelesaian
= bilangan titik persilangan
= 3