6.5.1 Rumus bagi sin (A ± B), kos (A ± B), tan (A ± B), sin 2A, kos 2A, tan 2A
(Contoh Soalan)
Contoh 2:
Buktikan setiap identity trigonometri yang berikut.
\(\begin{array}{l}\text{(a)}\frac{1+kos2x}{\sin2x}=kotx\\\text{(b)}kotA\mathrm{sek}2A=kotA+\tan2A\\\text{(c)}\frac{sinx}{1-kosx}=kot\frac x2\end{array}\)
Penyelesaian:
(a)
\(\begin{array}{l}Sebelah\text{ }kiri\\=\frac{1+kos2x}{\sin2x}\\=\frac{1+{(2kos^2x-1)}}{2\sin xkosx}\\=\frac{\cancel2kos^\cancel2x}{\cancel2\sin x\cancel{kosx}}\\=\frac{kosx}{\sin x}\\=kotx=Sebelah\text{ }kanan\end{array}\)
(b)
\(\begin{array}{l}Sebelah\text{ }kanan\\=kotA+\tan2A\\=\frac{kosA}{\sin A}+\frac{\sin2A}{kos2A}\\=\frac{kosAkos2A+\sin A\sin2A}{\sin Akos2A}\\=\frac{kosA{(kos^2A-\sin^2A)}+\sin A{(2\sin AkosA)}}{\sin Akos2A}\\=
\frac{kos^3A-kosA\sin^2A+2\sin^2AkosA}{\sin Akos2A}\\=\frac{kos^3A+kosA\sin^2A}{\sin Akos2A}\\=\frac{kosA{(kos^2A+\sin^2A)}}{\sin Akos2A}\\=\frac{kosA}{\sin Akos2A}\leftarrow\boxed{\sin^2A+kos^2A=1}\\={(\frac{kosA}{\sin A})}{(\frac1{kos2A})}\\=kotA\mathrm{sek}2A\\=Sebelah\text{ }kiri\end{array}\)
(c)
\(\begin{array}{l}Sebelah\text{ }kiri\\=\frac{sinx}{1-kosx}\\=\frac{2sin\frac x2kos\frac x2}{1-{(1-2sin^2\frac x2)}}\leftarrow\boxed{\begin{array}{l}\sin x=2sin\frac x2kos\frac x2,\\kosx=1-2\sin^2\frac x2\end{array}}\\=\frac{\cancel2\cancel{sin\frac x2}kos\frac x2}{\cancel2sin^\cancel2\frac x2}=\frac{kos\frac x2}{sin\frac x2}\\=kot\frac x2=Sebelah\text{ }kanan\end{array}\)
Contoh 3:
(a) Diberi bahawa
\(\sin P=\frac35\text{ dan }\sin Q=\frac5{13},\)
dengan keadaan P ialah satu sudut tirus dan Q ialah satu sudut cakah, tanpa menggunakan sifir atau kalkulator, cari nilai kos (P + Q).
(b) Diberi bahawa
\(\sin A=-\frac35\text{ dan }\sin B=\frac{12}{13},\)
dengan keadaan A dan B adalah sudut-sudut dalam sukuan III dan sukuan IV masing-masing, tanpa menggunakan sifir atau kalkulator, cari nilai sin (A – B).
(a)
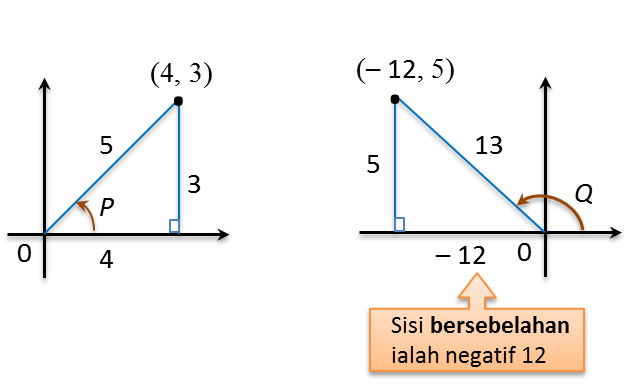

\(\begin{array}{l}\sin P=\frac35,kosP=\frac45\\\sin Q=\frac5{13},kosQ=-\frac{12}{13}\\\\kos{(P+Q)}\\=kosAkosB-\sin A\sin B\\={(\frac45)}{(-\frac{12}{13})}-{(\frac35)}{(\frac5{13})}\\=-\frac{48}{65}-\frac{15}{65}\\=-\frac{63}{65}\end{array}\)
(b)
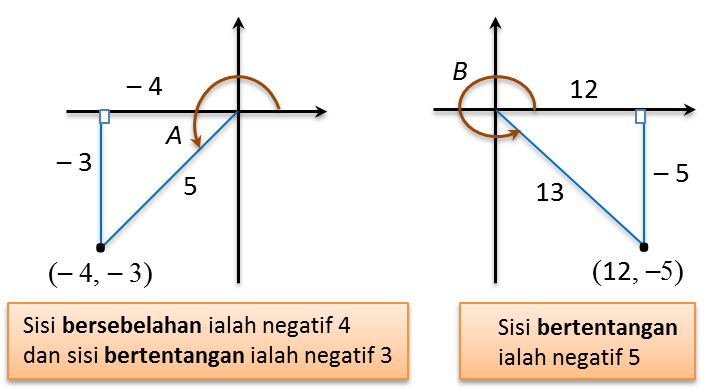

\(\begin{array}{l}\sin A=-\frac35,kosA=-\frac45\\\sin B=-\frac5{13},kosB=\frac{12}{13}\\\\sin{(A-B)}\\=sinAkosB-kosA\sin B\\={(-\frac35)}{(\frac{12}{13})}-{(-\frac45)}{(-\frac5{13})}\\=-\frac{36}{65}-\frac{20}{65}\\=-\frac{56}{65}\end{array}\)