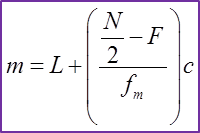7.1c Median
1. Median ialah nilai yang terletak di tengah-tengah sesuatu set data setelah set data itu disusun mengikut tertib tertentu.
(A) Data Tak Terkumpul
Contoh 1:
Cari median bagi setiap set data yang berikut.
(a) 15, 18, 21, 25, 20, 18
(b) 13, 6, 9, 17, 11
Penyelesaian:
(a)
Susun data mengikut tertib menaik
15, 18, 18, 20, 21, 25
(b)
6, 9, 11, 13, 17
(B) Data Terkumpul (tanpa Selang Kelas)
Contoh 2:
Jadual kekerapan yang berikut menunjukkan markah ujian biologi bagi 40 orang pelajar.

Hitung markah median.
Penyelesaian:
(C) Data Terkumpul (dengan Selang Kelas)
m = median
L = sempadan bawah kelas median
N = jumlah kekerapan
F = kekerapan longgokan sebelum kelas median
fm = kekerapan kelas median
c = saiz kelas median (Sempadan atas kelas – sempadan bawah kelas)
1. Median boleh ditentukan daripada jadual kekerapan longgokan dan ogif.
Contoh 3:
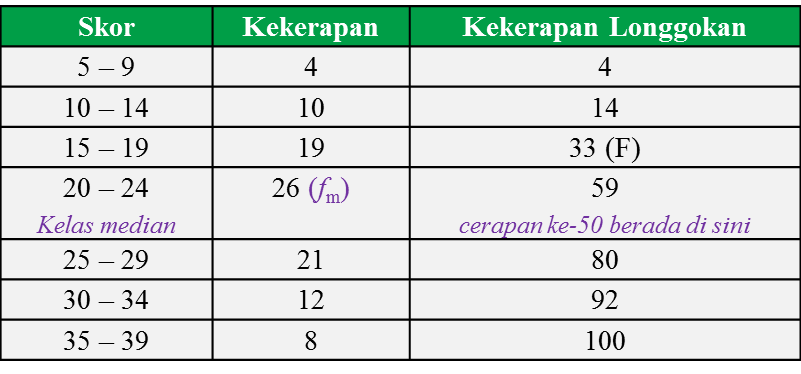
Jadual yang berikut menunjukkan taburan skor yang diperoleh 100 orang pelajar tingkatan 4 dalam satu pertandingan.

Cari median.
Penyelesaian:
Kaedah 1: guna rumus

Langkah 1:
Langkah 2: